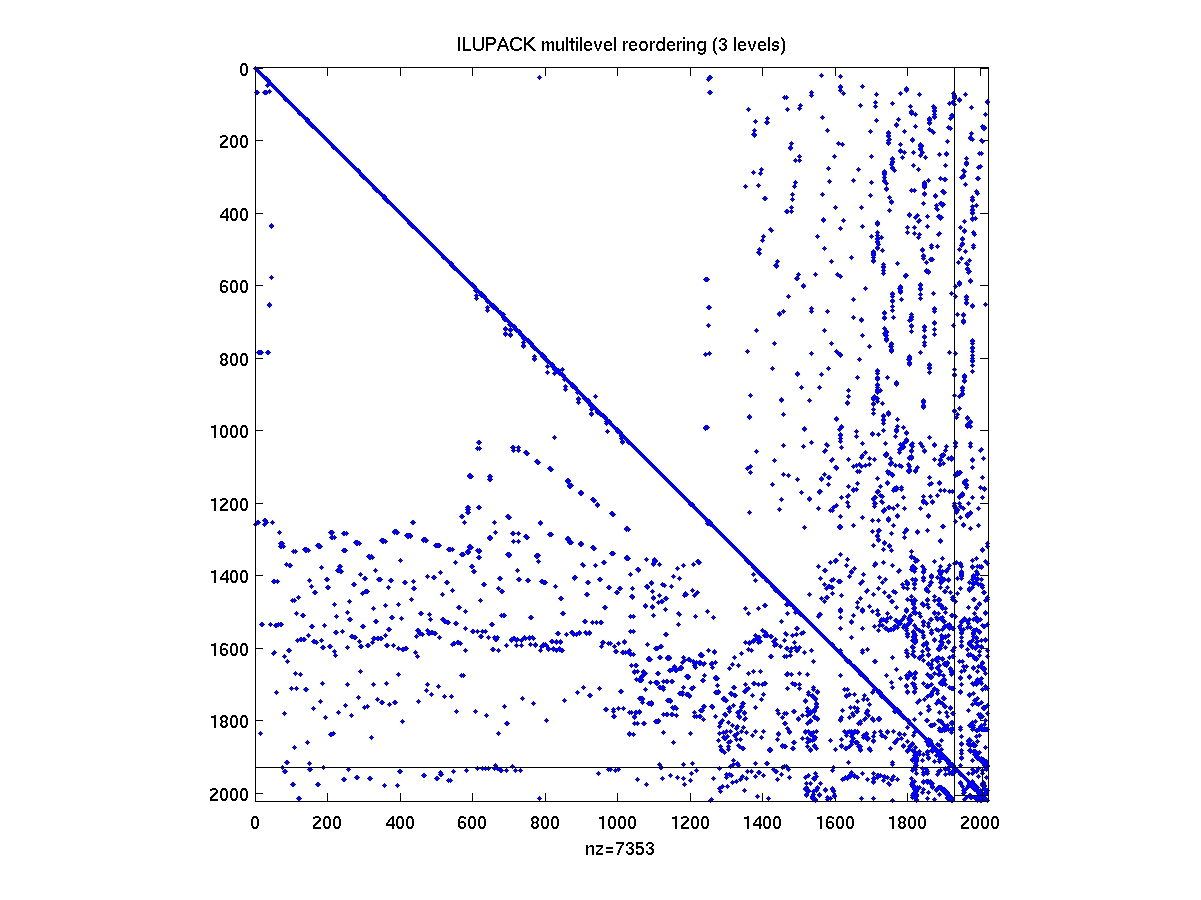
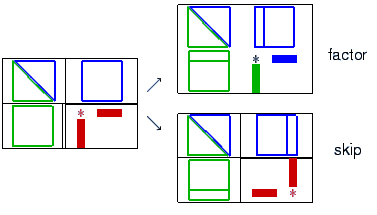
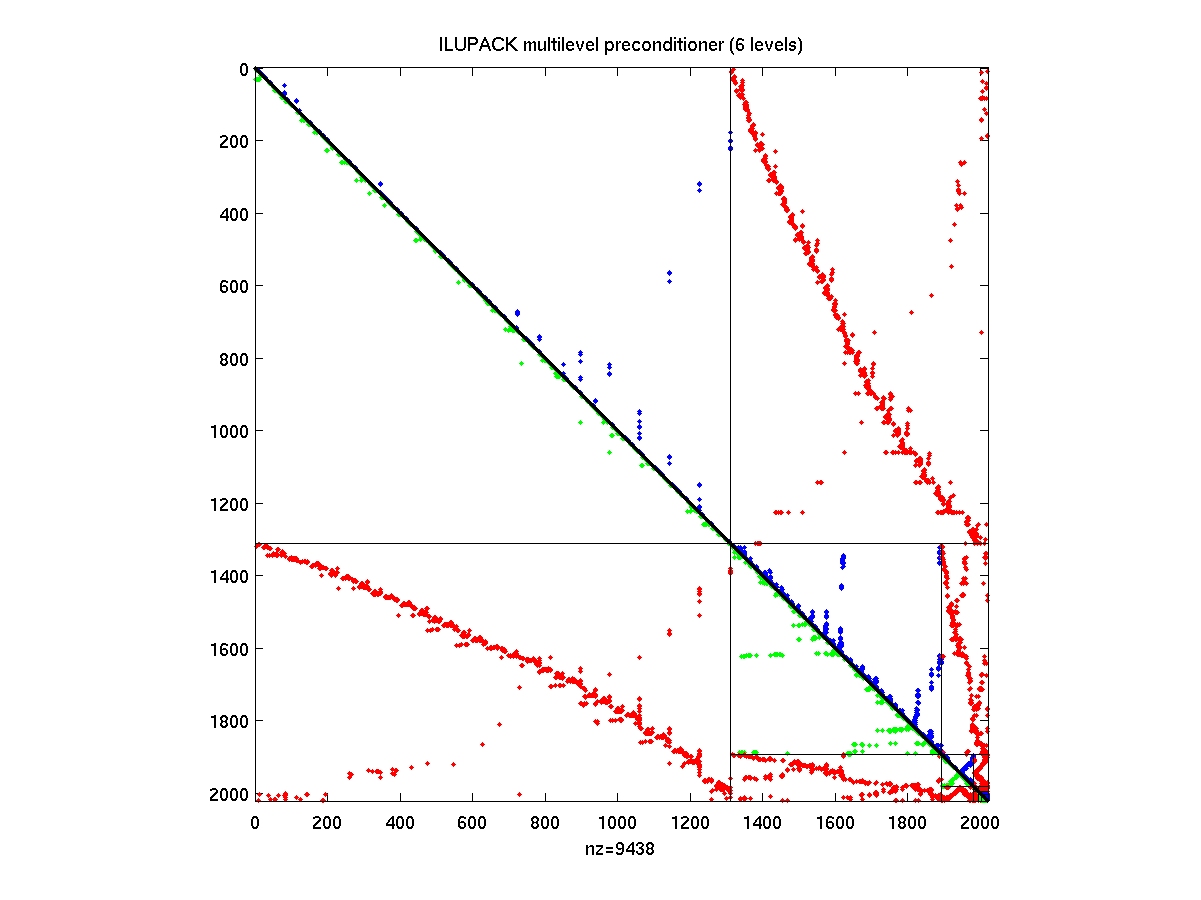
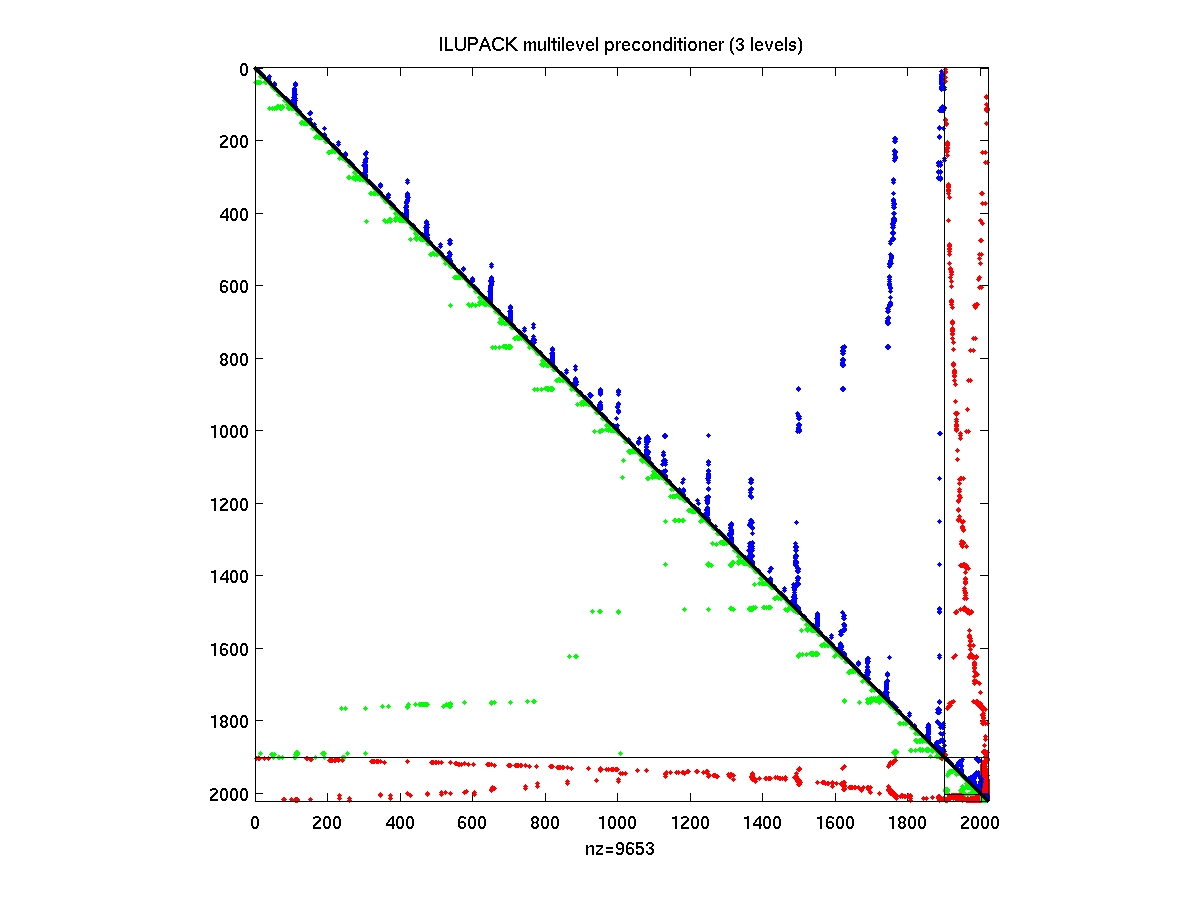
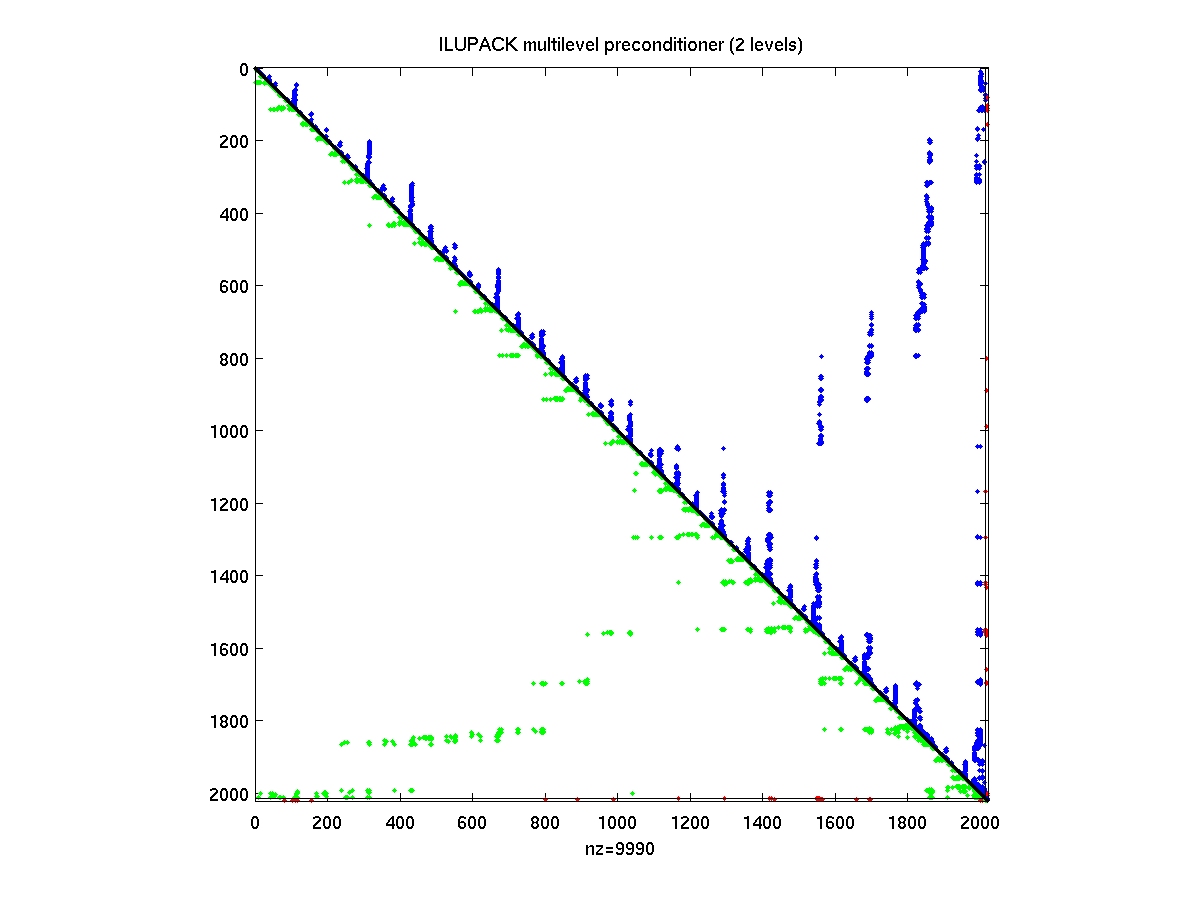
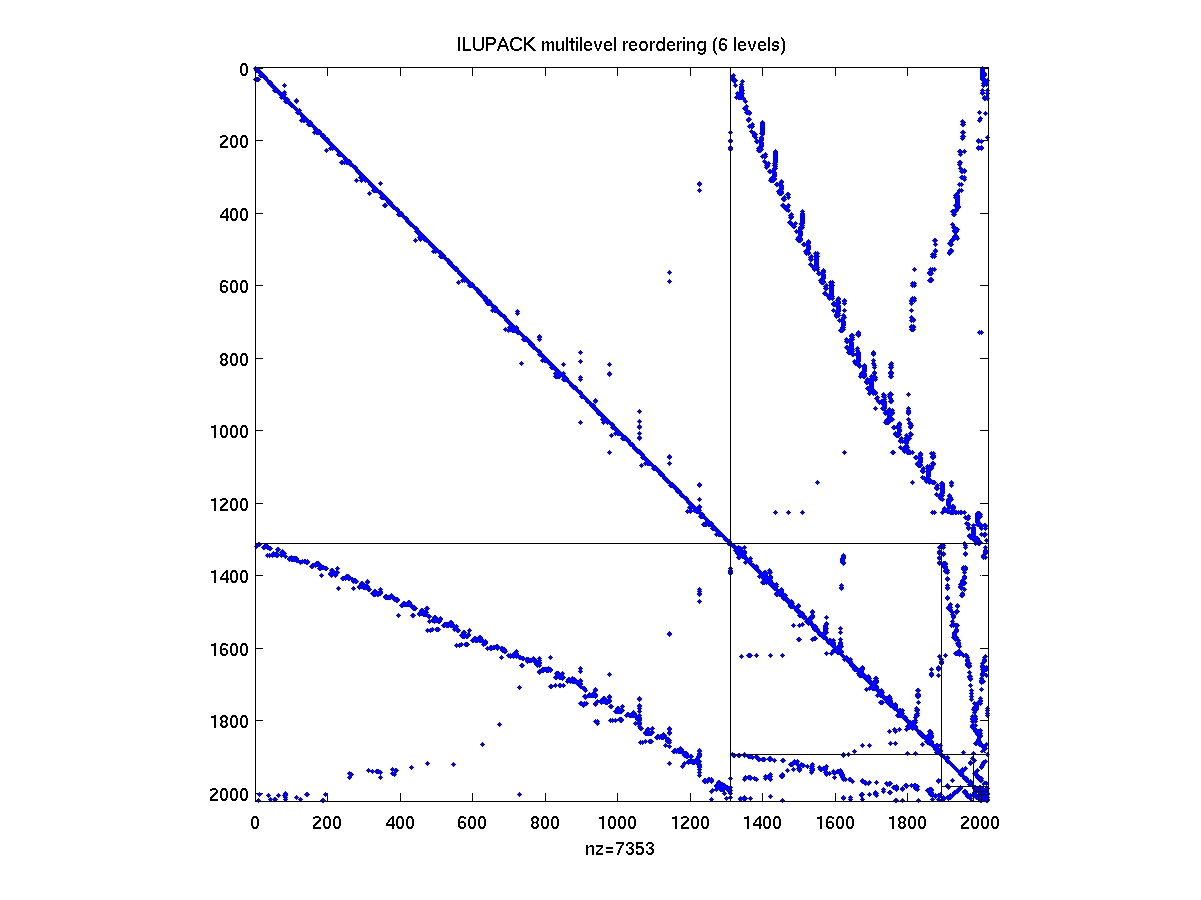
After compiling the mex interface drivers from the ILUPACK directory,
add the associated system path, e.g., using the MATLAB command
If you do not need the preconditioner anymore discard it using AMGdelete.
The main philosophy of ILUPACK can be summarized in three major components.
ILUPACK offers many, many parameters that you may alter.
Some parameters you will find familiar, others may confuse you ...
|
matching
|
improve diagonal dominance using maximum weighted matchings
|
|
ordering
|
preprocess the system by a symbolic reordering
(e.g. 'amd', Approximate Minimum Degree)
|
|
droptol
|
threshold to drop small entries during the factorization
|
|
droptolS
|
threshold to drop small entries from the Schur complement (coarse grid system)
|
|
droptolc
|
threshold for dropping small entries from the constraint part,
if present
|
|
condest
|
bound for the inverse triangular factors
|
|
restol
|
stopping criterion for the iterative process (backwar error)
|
|
maxit
|
maximum number of iteration steps
|
|
elbow
|
memory space to keep the preconditioner (relative to the number
of nonzeros of A)
|
|
lfil
|
number of nonzeros per row in the approximate factorization
|
|
lfilS
|
number of nonzeros per row in the approximate Schur complement
|
|
typetv
|
kind of test vector (default 'none', alternatively 'static' for providing a vector for which the multilevel ILU is exact)
|
|
tv
|
test vector such that the factorization is exact for this vector
|
|
amg
|
kind of multilevel method (default: 'ilu' no inner iteration on the Schur complement system, alternatively 'amli' for inner iteration or 'mg' for multigrid-like set up
|
|
npresmoothing
|
number of pre smoothing steps (if param.amg='mg' is chosen)
|
|
npostsmoothing
|
number of post smoothing steps (if param.amg='mg' is chosen)
|
|
ncoarse
|
number of coarse grid correction steps (only if param.amg='amli' or 'mg' is chosen)
|
|
presmoother
|
type of pre smoother (e.g. 'gsf' Gauss-Seidel forward, only if param.amg='mg' is chosen)
|
|
postsmoother
|
type of post smoother (e.g. 'gsb' Gauss-Seidel backward, only if param.amg='mg' is chosen)
|
|
FCpart
|
decide whether nodes should be grouped a priori into
some 'fine' grid nodes or 'coarse' grid nodes (default 'none')
|
|
typecoarse
|
type of coarse grid system (define how the approximation is computed, e.g. 'ilu' is the easiest and fastest but least accurate coarse grid system)
|
|
solver
|
which iterative solver is used (e.g. 'gmres')
|
|
damping
|
damping factor for Jacobi smoothing
|
|
nrestart
|
number of steps before GMRES is restarted
|
|
ind
|
indicator array to indicate saddle point structure
|
|
isdefinite
|
tell ILUPACK in advance that you matrix is positive definite
|
|
mixedprecision
|
compute preconditioner in single precision
|
|
contraction
|
contraction factor of the residual for inner flexible solver when AMLI or
classical multigrid is used
|
|
coarsereduce
|
If different from zero, then the L21 and the U12 block
are discarded solving with L,U is done implicitly via L11,U11 and
A21 (resp. A12).
|
|
decoupleconstraints
|
This allows for saddle point type problems to explictly
decouple the connections between the constraint part and the
free part.
|
However, ILUPACK asks YOU to provide whether the system is positive definite
or not. You can do that by setting options.isdefinite before
you factor your matrix, e.g.
ILUPACK offers YOU a tool to convert a symmetric
preconditioner into a positive definite one using AMGconvert.
This has to be done, after the preconditioner is built, e.g.
- AMGinit
options = AMGinit(A)
options = AMGinit(A,options)
init structure of options to their default values for a given nxn matrix A
input
-----
A nxn matrix
options optional input to indicate via options.isdefinite that your
matrix is positive definite
output
------
options structure with default parameters
------------------------------------------------------------------------
possible options:
1. options.matching
--------------------
if different from zero then maximum weight matching will be used,
for the real symmetric, complex Hermitian or complex symmetric the
associated symmetric maximum weight matching will be used.
`maximum weight matching' is a technique to reorder and rescale the
matrix such that it is becomes more diagonally dominant
default value: 1
2. options.ordering
--------------------
several reorderings based on |A|+|A|' are offered. Unsymmetric patterns
treated as if they were symmetric.
The orderings are repeated on any coarser level.
`amd' default, Approximate Minimum Degree
`metisn' METIS multilevel nested dissection by NODES
`metise' METIS multilevel nested dissection by EDGES
`rcm' Reverse Cuthill-McKee
`mmd' Minimum Degree
`amf' Approximate Minimum Fill
any other no reordering
3. options.droptol
-------------------
threshold for dropping small entries during the computation of the
incomplete LU decomposition
default: 1e-2
4. options.droptolS
--------------------
threshold for dropping small entries from the Schur complement
default: 1e-2
5. options.droptolc
--------------------
threshold for dropping small entries from the constraint part,
if present (as indicated by negative entries in options.ind)
default: 0
6. options.condest
-------------------
bound for the inverse triangular factors from the incomplete LU
decomposition
default: 100
7. options.restol
------------------
bound for the accuracy of the approximate solution of Ax=b for a given
right hand side after using ILUPACK-preconditioned iterative solution
This tolerance refers to the BACKWARD ERROR, in the symmetric(Hermitian)
positive definite case to the relative error in the energy norm
default: sqrt(eps)
8. options.maxit
-----------------
maximum number of iteration steps, before the iterative ILUPACK-
preconditioned solvers terminates
default: 500
10. options.elbow
-----------------
elbow space for memory of the ILUPACK multilevel preconditioner.
Since the core part of the code is FORTRAN 77, no dynamic memory
allocation is available, one has to estimate the memory requirement
in advance by multiples of the fill of the initial matrix
default: 10 (ten times as much fill as the initial matrix)
11. options.lfil
---------------
restrict the number of nonzeros per column in L (resp. per row in U)
hard to at most `lfil' entries.
default: n+1
12. options.lfilS
----------------
restrict the number of nonzeros per row in the approximate Schur
complement hard to at most `lfilS' entries.
default: n+1
13. options.typetv
------------------
define, whether to include a test vector into the computations
If used, then (a) the test vector is also included to estimate
the norm of the inverse triangular factors
(b) it is used to obtain a refined fine/coarse
grid partitioning (if switch is set)
(c) diagonal compensation and off-diagonal lumping
are added to improve the factorization
default: 'none'
alternatives: 'static' for a fixed test vector
'function_name' for a dynamically generated test
vector the user has to provide a
custom routine to generate the test
vector
format:
tvd=function_name(mat,tv_old)
On every level the associate matrix
'mat' is passed to this routine,
also the coarse grid projection of
the previous test vector 'tv_old' from
the finer grid is passed. On exit, 'tvd'
is the dynamic test vector that should be
used
13. options.tv
--------------
static test vector. Ignored if options.typetv=='none'
If options.typetv=='function_name', then on the initial finest level,
options.tv is passed to 'function_name' as initial guess for 'tv_old'
14. options.amg
---------------
type of AMG preconditioner
default: 'ilu' multilevel ILU
alternatives: 'amli' multilevel ILU, where on each coarser grid
an inner iteration is used to solve the
coarse grid system. The number of inner
interation steps is prescribed in
options.ncoarse
'mg' classical multigrid with pre and post
smoothing
15. options.npresmoothing
-------------------------
number of pre smoothing steps (only needed if options.amg=='mg')
default: 1
16. options.npostsmoothing
--------------------------
number of post smoothing steps (only needed if options.amg=='mg')
default: 1
17. options.ncoarse
-------------------
number of coarse grid correction steps (only needed if options.amg=='mg'
or options.amg=='amli')
default: 1
if a negative value is used, then a flexible solver is used.
18. options.presmoother
-------------------------
type of pre smoother
default: 'gsf' Gauss-Seidel forward
'gsb' Gauss-Seidel backward
'j' Jacobi
'ilu' partial incomplete ILU on the F-nodes
'function_name' custom routine for smoothing
d=function_name(mat,r)
Given the matrix 'mat' on each level
and the associated residual
'r(=b-mat*x_old)', the custom smoother
is asked to compute an approximate defect
'd' such that x_new=x_old+d
19. options.postsmoother
-------------------------
type of post smoother
default: 'gsb' Gauss-Seidel backward
'gsf' Gauss-Seidel forward
'j' Jacobi
'ilu' partial incomplete ILU on the F-nodes
'function_name' custom routine for smoothing
d=function_name(mat,r)
Given the matrix 'mat' on each level
and the associated residual
'r(=b-mat*x_old)', the custom smoother
is asked to compute an approximate defect
'd' such that x_new=x_old+d
20. options.FCpart
------------------
preselect a partitioning into fine grid and coarse grid nodes
default: 'none'
'yes' if F/C partioning is desired
21. options.typecoarse
----------------------
type of coarse grid system
default: 'ilu' coarse grid system is computed from the
approximate incomplete factorization by
ignoring that entries have been discarded
'amg' Use the associated approximate interpolation
operator P and the restriction operator R
from the underlying inverse triangular
factors to generate the Galerkin type
coarse grid matrix R A P
22. options.damping
----------------------
damping factor if Jacobi smoothing is chosen
23. options.isdefinite
----------------------
if given on input then the matrix is assumed to be symmetric (Hermitian)
positive definite and the parameters will be
24. options.ind
---------------
indicate by negative signs which parts of the system refer to the
second (typically) zero block of a saddle point system
25. options.mixedprecision
---------------
if different from zero, then single precision for preconditioning is
used
26. options.contraction
-----------------------
contraction of the residual for inner flexible solver when AMLI or
classical multigrid is used and options.ncoarse<0 (flexible coarse
grid solver)
27. options.coarsereduce
------------------------
default: 1. If different from zero, then the L21 and the U12 block
are discarded solving with L,U is done implicitly via L11,U11 and
A21 (resp. A12). If set to zero, then L21, U12 are kept
28. options.decoupleconstraints
-------------------------------
default: 1. This allows for saddle point type problems to explictly
decouple the connections between the constraint part and the
free part. Applied on every level, this allows for smaller coarse
grid matrices. If set to zero, then the additional decoupling is
not applied
- AMGfactor
[PREC, options] = AMGfactor(A, options);
[PREC, options] = AMGfactor(A);
Computes ILUPACK preconditioner PREC according to the given options.
For details concerning `options' see `AMGinit'
input
-----
A nxn nonsingular matrix
options parameters. If `options' is not passed then the default options
from `AMGinit' will be used
output
------
PREC ILUPACK multilevel preconditioner
PREC is a structure of `nlev=length(PREC)' elements indicating
the number of levels.
For every level l we have
PREC(l).n size of level l
PREC(l).nB size of the leading block of level l
PREC(l).L (block) lower triangular matrix
PREC(l).D (block) diagonal matrix
PREC(l).U if present: (block) upper triangular matrix
for symmetrically structured matrices only
L is present.
L*D^{-1}*U
is the approximate LU decomposition of the
leading block of A after rescaling and
reordering
PREC(l).E except for l
- AMGsolver, AMGhsolver, AMGtsolver
[x, options] = AMGsolver(A, PREC, options, b, x0)
[x, options] = AMGsolver(A, PREC, options, b)
[x, options] = AMGsolver(A, PREC, b, x0)
[x, options] = AMGsolver(A, PREC, b)
Solves Ax=b using ILUPACK preconditioner PREC according to the given options
[x, options] = AMGhsolver(A, PREC, options, b, x0)
[x, options] = AMGhsolver(A, PREC, options, b)
[x, options] = AMGhsolver(A, PREC, b, x0)
[x, options] = AMGhsolver(A, PREC, b)
Solves A'x=b, where A' is the (conjugate) transposed matrix
w.r.t. A. This is done using ILUPACK preconditioner PREC
according to the given options
[x, options] = AMGtsolver(A, PREC, options, b, x0)
[x, options] = AMGtsolver(A, PREC, options, b)
[x, options] = AMGtsolver(A, PREC, b, x0)
[x, options] = AMGtsolver(A, PREC, b)
Solves A.'x=b, where A.' is the transposed matrix w.r.t. A.
This is done using ILUPACK preconditioner PREC according
to the given options
- AMGdelete
PREC=AMGdelete(PREC)
delete preconditioner, in particular release the associated memory
- AMGsol, AMGhsol, AMGtsol
x = AMGsol(PREC,b)
Solves Ax=b using one step of the computed ILUPACK preconditioner PREC
x = AMGhsol(PREC,b)
For general nonsymmetric and non-Hermitian matrices A, this routine
solves A'x=b where A' is the conjugate transposed matrix w.r.t. A.
This is done using one step of the computed ILUPACK
preconditioner PREC
x = AMGtsol(PREC,b)
For general nonsymmetric and non-Hermitian matrices A, this routine
solves A.'x=b, where A.' is the transposed matrix w.r.t. A.
This is done using one step of the computed ILUPACK
preconditioner PREC
- AMGnnz
nz=AMGnnz(PREC)
total number of nonzeros of the multilevel ILU
to be consistent with MATLAB, the preconditioner is
treated as if it were unsymmetric
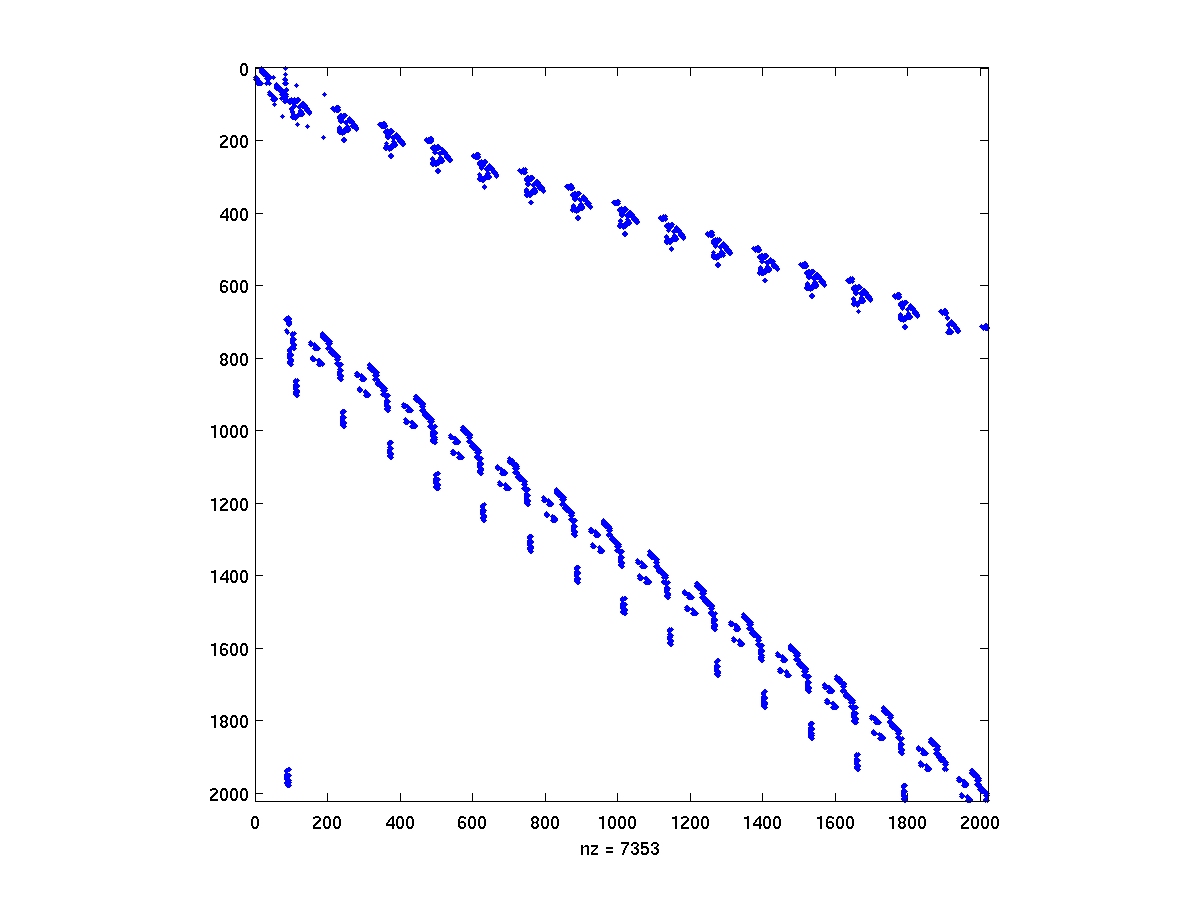
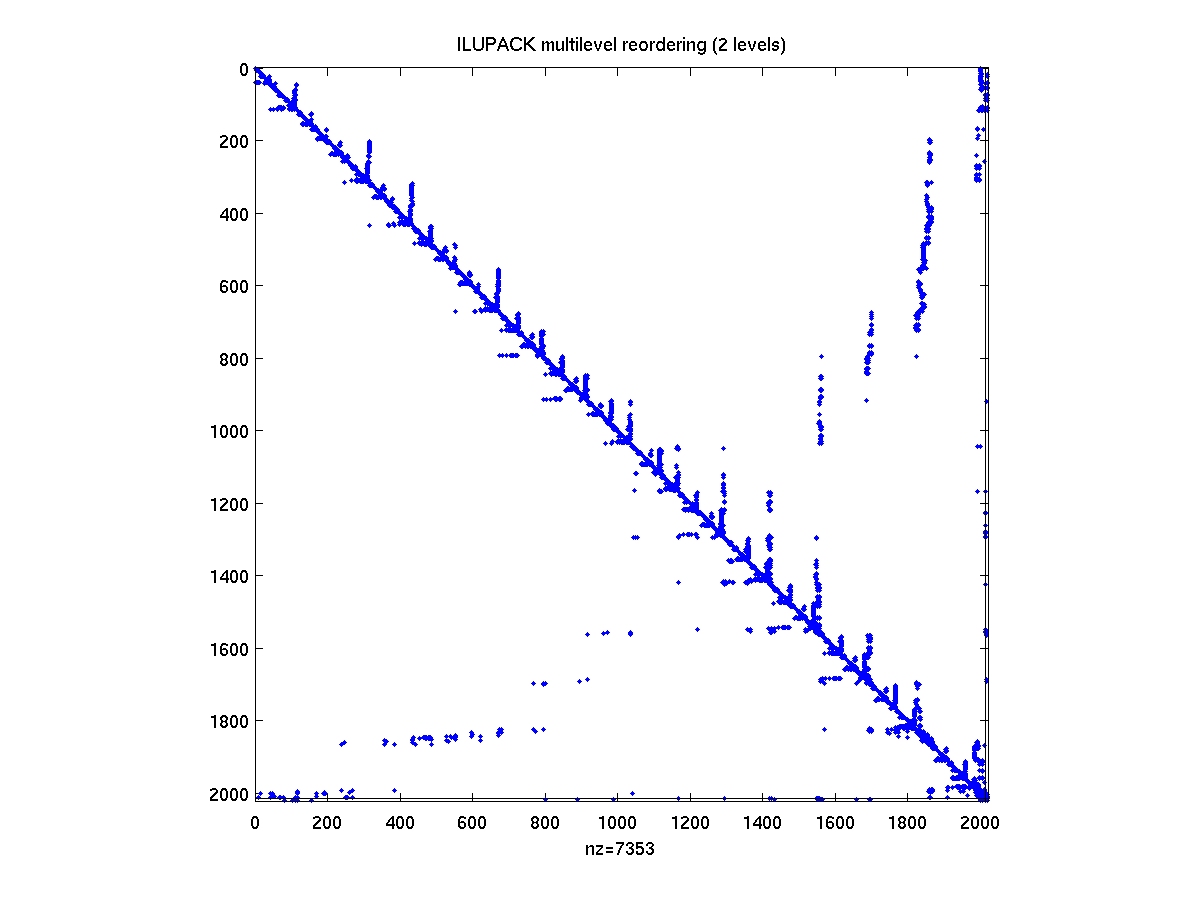
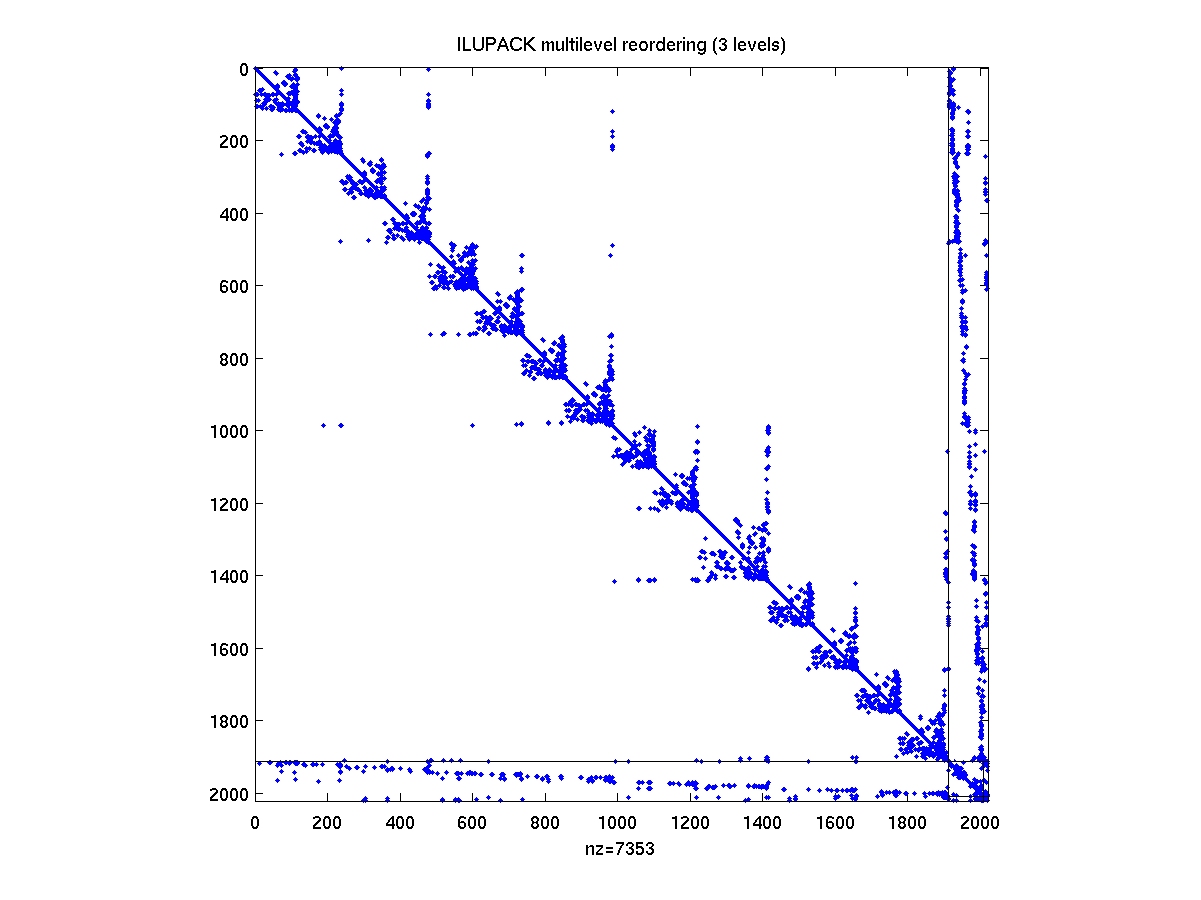
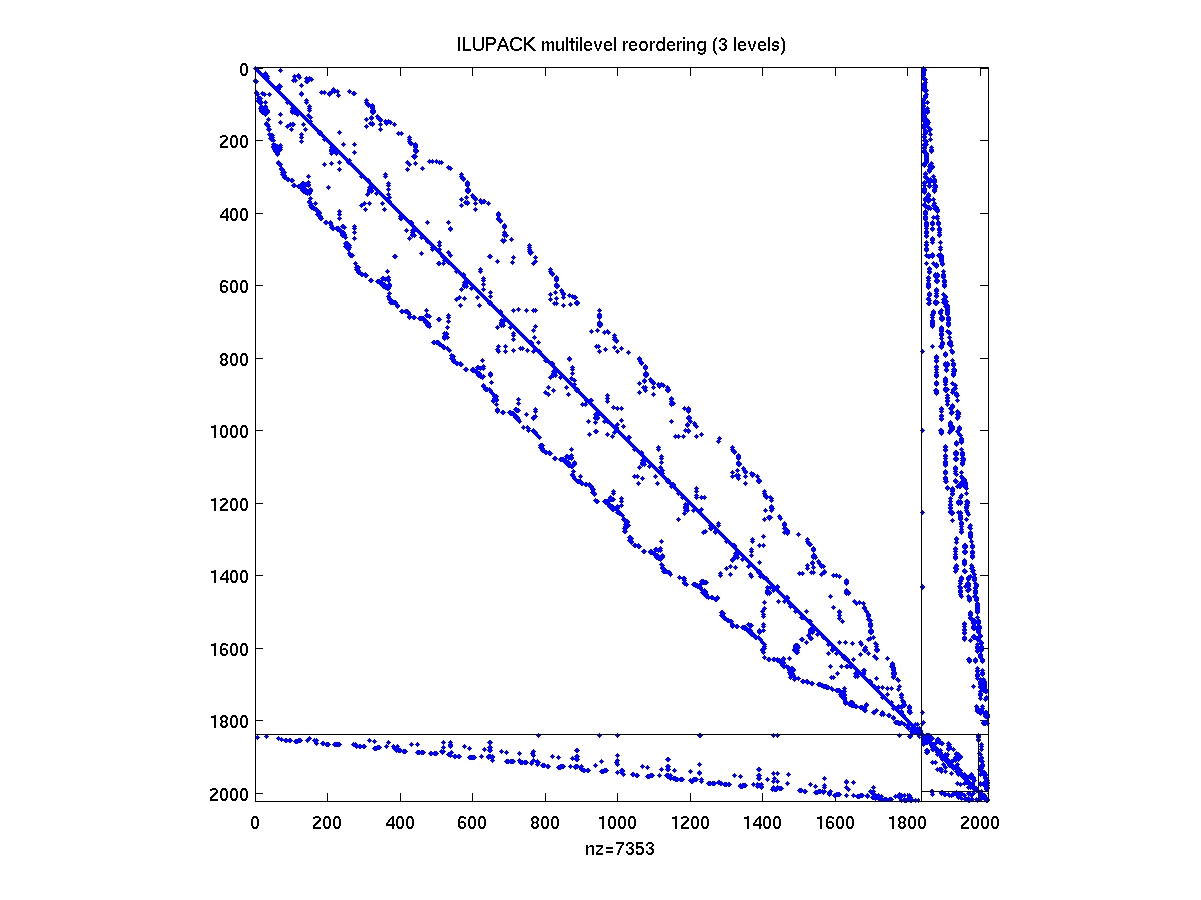
- AMGspy
AMGspy(PREC)
display multilevel preconditioner PREC
AMGspy(A,PREC)
display remapped original matrix A associated with the sequence of
reorderings given by PREC
- AMGconvert
PREC = AMGconvert(PREC)
If the preconditioner is real symmetric and indefinite or complex Hermitian
and indefinite, then this routine turns PREC into a positive definite preconditioner
- loadhbo / savehbo
[A,rhs,rhstyp]=loadhbo(filename)
load matrix A and optionally right hand side b, initial guess x0 and
exact solution x
Input
-----
filename name of the file without extension
Output
------
A mxn sparse matrix
rhs vector of right hand side(s), initial guess(es), exact solution(s)
depending on `rhstyp'
rhstyp rhstyp(1)=='F' or rhstyp=='f'
=> dense right hand side(s)
rhstyp(2)=='G' or rhstyp=='g'
=> dense initial guess(es)
rhstyp(2)=='X' or rhstyp=='g'
=> dense exact solution(s)
depending on rhstyp it will be clear how many columns of `rhs'
correspond to the hand side(s), the initial guess(es) or the exact
solution(s)
savehbo(filename, A)
savehbo(filename, A,b)
savehbo(filename, A,b,x0)
savehbo(filename, A,b,x0,x)
save matrix A and optionally right hand side b, initial guess x0 and
exact solution x
- mwm / mwmamd / mwmmetisn / mwmmetise / mwmmmd / mwmrcm
[pl,pr,Dl,Dr] = mwm(A)
reorder and rescale a given nxn matrix A using maximum weight
matching
input
-----
A n x n matrix
output
------
pl,pr left and right permutation vectors
Dl, Dr left and right scaling matrices
On exit B=Dl*A(pl,pr)*Dr would refer to the reordered
and rescaled system such that in theory |B(i,i)|=1
and |B(i,j)|<=1. In practice, powers of 2 are used for
scaling matrices Dl,Dr to avoid rounding errors. For
this reason, the scaled entries fulfill the constraint
only within the range that can be achieved by the nearest
power of 2 for Dl,Dr
[pl,pr,Dl,Dr] = mwmamd(A)
reorder and rescale a given nxn matrix A using maximum weight
matching followed by approximate minimum degree
[pl,pr,Dl,Dr] = mwmmetisn(A)
reorder and rescale a given nxn matrix A using maximum weight
matching followed by Metis Nested Dissection by nodes
[pl,pr,Dl,Dr] = mwmmetise(A)
reorder and rescale a given nxn matrix A using maximum weight
matching followed by Metis Nested Dissection by edges
[pl,pr,Dl,Dr] = mwmmmd(A)
reorder and rescale a given nxn matrix A using maximum weight
matching followed by Minimum Degree
[pl,pr,Dl,Dr] = mwmrcm(A)
reorder and rescale a given nxn matrix A using maximum weight
matching followed by reverse Cuthill-McKee
- symmwmamd / symmwmmetisn / symmwmmetise / symmwmmmd / symmwmrcm
[p,D] = symmwmamd(A)
reorder and rescale a given nxn SYMMETRIC/HERMITIAN matrix A using symmetric
maximum weight matching followed by approximate minimum degree
input
-----
A nxn matrix
output
------
p permutation vector. On exit D*A(p,p)*D refers to the reordered
and rescaled system
[p,D] = symmwmmetisn(A)
reorder and rescale a given nxn SYMMETRIC/HERMITIAN matrix A using symmetric
maximum weight matching followed by METIS multilevel nested dissection by nodes
[p,D] = symmwmmetise(A)
reorder and rescale a given nxn SYMMETRIC/HERMITIAN matrix A using symmetric
maximum weight matching followed by METIS multilevel nested dissection by edges
[p,D] = symmwmmmd(A)
reorder and rescale a given nxn SYMMETRIC/HERMITIAN matrix A using symmetric
maximum weight matching followed by minimum degree
[p,D] = symmwmrcm(A)
reorder and rescale a given nxn SYMMETRIC/HERMITIAN matrix A using symmetric
maximum weight matching followed by Reverse Cuthill-McKee
- symmetisn / symmetise
p = symmetisn(A)
reorder a given nxn matrix A using METIS multilevel nested dissection
by nodes
input
-----
A nxn matrix
output
------
p permutation vector. On exit A(p,p) refers to the reordered
system
p = symmetise(A)
reorder a given nxn matrix A using METIS multilevel nested dissection
by edges
- sqmr
[x,flag,iter,resvec]=sqmr(A,b,tol,maxit,M1,M2,x0)
sQMR simplified Quasi-Minimal Residual Method for symmetric matrices A
symmetric preconditioning.
x = sqmr(A,b) attempts to solve the system of linear equations A*x=b for
x. The n-by-n coefficient matrix A must be square and real symmetric (resp.
complex Hermitian or complex symmetric) and the right hand
side column vector b must have length n.
x = sqmr(A,b,tol) specifies the tolerance of the method. If tol not
specified, then sqmr uses the default, 1e-6.
x = sqmr(A,b,tol,maxit) specifies the maximum number of iterations. If
maxit is not specified then sqmr uses the default, min(N,500).
x = sqmr(A,b,tol,maxit,M) and x = sqmr(A,b,tol,maxit,M1,M2) use
preconditioners M or M=M1*M2 and effectively solve the system
inv(M)*A*x = inv(M)*b for x. M may be a function handle mfun such that
mfun(x) returns M\x.
x = sqmr(A,b,tol,maxit,M1,M2,x0) and x=sqmr(A,b,tol,maxit,M,x0) specifies
the initial guess. If x0 is not specified then sqmr uses the zero vector.
[x,flag] = sqmr(A,b,...) also returns a convergence flag:
0 sqmr converged to the desired tolerance tol within maxit iterations.
As stopping criterion the backward error ||Ax-b||/(||A|| ||x||+||b||)
is used
1 sqmr iterated maxit times but did not converge.
2 break down
-m unknown error code
[x,flag,iter] = sqmr(A,b,...) also returns the iteration number
at which x was computed: 0 <= iter <= maxit.
[x,flag,iter,resvec] = sqmr(A,b,...) also returns a vector of the
estimated residual norms at each iteration, including norm(b-A*x0).