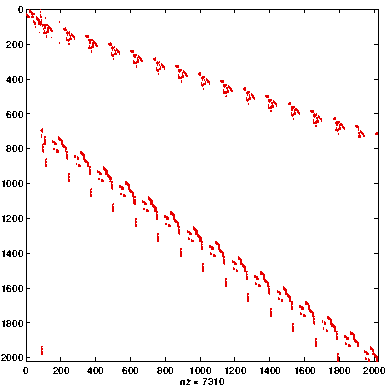
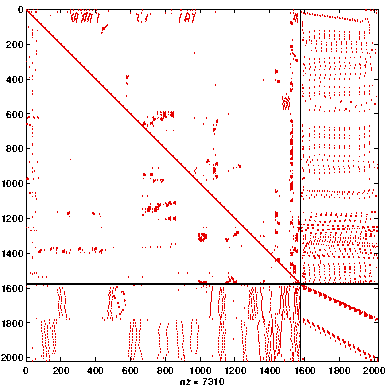
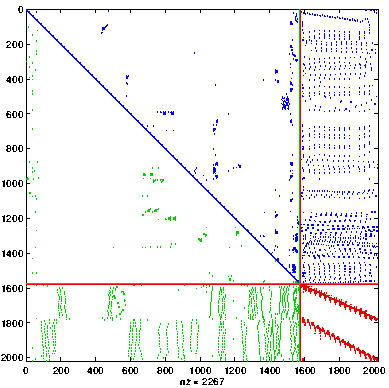
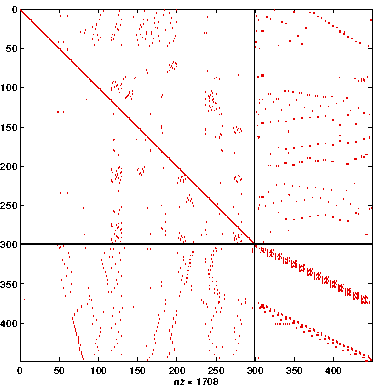
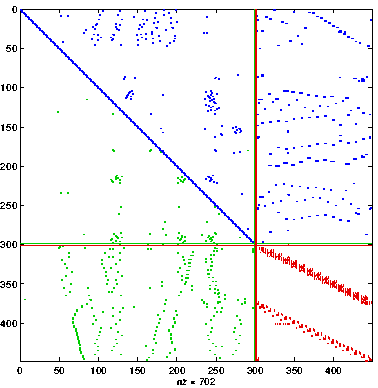
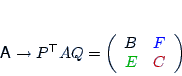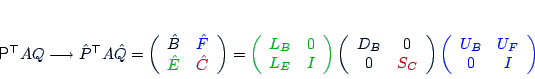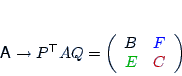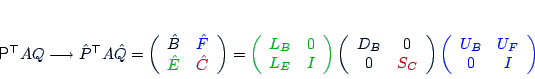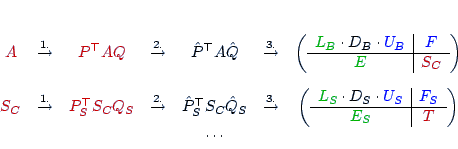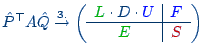Multilevel Algorithms

Sketch of the Templates

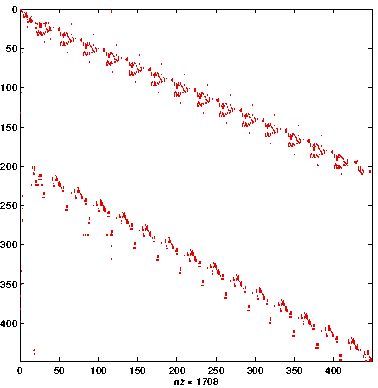
  1. Compute a static partial reordering

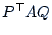    \begin{displaymath} % latex2html id marker 1048A \to P^\top AQ = \left( \begi... ...\ \textcolor{green}{E}& \textcolor{red}{C} \end{array}\right) \end{displaymath}

     

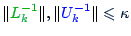  2. Factor $P^\top AQ$ and control % latex2html id marker 1056 $\Vert\textcolor{green}{L_k^{-1}}\Vert,\Vert\textcolor{blue}{U_k^{-1}}\Vert\leqslant\kappa$.
    \begin{displaymath} % latex2html id marker 1049P^\top AQ \longrightarrow \hat ... ...eft( \begin{array}{cc} U_B & {U_F}\\ 0& I \end{array}\right)} \end{displaymath}

     

  3. Apply strategy recursively to the approximate Schur complement (multilevel scheme)


Sketch of the Templates

west2021_org west2021_lev1start west2021_lev1end
west2021_lev2org west2021_lev2start west2021_lev2end

m.bollhoefer@tu-bs.de

Last modified: October 11, 2011