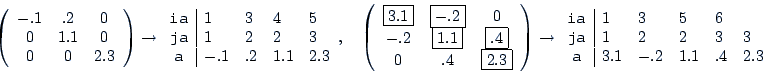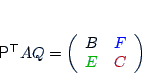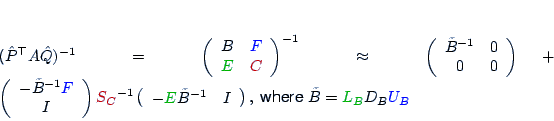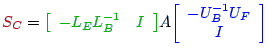| param.matching |
use matching (1, default) or not (0) |
| param.ordering |
desired symmetric reordering
| "amd" (default) | Approximate Minimum Degree |
| "metisn" | Metis Multilevel Nested Dissection by nodes |
| "metise" | Metis Multilevel Nested Dissection by edges |
| "mmd" | Minimum Degree |
| "rcm" | Reverse Cuthill-McKee |
| "amf" | Approximate Minimum fill |
| "indset" | Independent sets |
| "pq" | ddPQ strategy from ARMS |
|
| param.droptol |
drop tolerance for the LU factors.
By default, 1e-2 is chosen. Here you can overwrite the default values.
|
| param.droptolS |
drop tolerance for the approximate Schur complement.
By default, 0.1*param.droptol is chosen and recommended. Here you can overwrite the default values.
|
| param.droptolc |
threshold for dropping small entries from the constraint part,
if present (as indicated by negative entries in options.ind)
default: 0
|
| param.condest |
Norm of the inverse triangular factors.
by default, 5 is chosen. Here you can overwrite the default values.
As a rule of thumb, small CONDEST will allow more entries to be dropped
(which may accelerate the computation and save memory) but at the same
time, more levels will be necessary (which in turn may slow down the
computation and increase the memory). Typically, values between 5 and
100 make sense.
CONDEST=5 will make ILUPACK behave like AMG and select many coarse grid
nodes. If you have a PDE-based problem, this might be the right choice.
Otherwise, CONDEST=100 will safeguard the ILU computation and prevent
the norm of the inverse triangular factors from becoming too large.
|
| param.restol |
Residual tolerance for the iterative solver.
The built-in iterative solver (CG/SQMR/restarted GMRES by default)
will use this
tolerance to terminate whenever the backward error (resp. relative energy norm) is less than this
threshold. By default, eps^(3/4)~1e-12 is chosen for double precision,
eps^(3/4)~1e-6 is chosen for single precision.
|
| param.elbow |
elbow space for the ILU.
Here please pass an estimate how much memory you are willing to spend.
ILUPACK will try to keep the ILU inside the range you passed. The elbow
space is a real number measuring the number of nonzeros of the ILU
relative to the fill of the original matrix. By default, 10 is chosen.
Note however, if your estimate is too small, ILUPACK will adapt elbow
and overwrite this parameter. As long as enough memory is available, the
ILU will be successfully computed.
|
| param.lfil |
Maximum number of nonzeros per column in L (resp. per row in
U).
By default n+1 is chosen, i.e. this option is disabled. You can limit
the amount of memory by using some smaller value, e.g. A.ia[A.nc]-1
is the fill of A and ELBOW*(A.ia[A.nc]-1.0)/A.nc would restrict the
maximum number of fill to the average number of nonzeros of A per column
(or per row) times the ELBOW. Note however that this parameter cuts off
the fill in L and U by brute force. It recommended NOT to use it.
|
| param.lfilS |
Maximum number of nonzeros per row in S (approximate Schur
complement).
By default n+1 is chosen, i.e. this option is disabled. You can limit
the amount of memory by using some smaller value, e.g. A.ia[A.nc]-1
is the fill of A and ELBOW*(A.ia[A.nc]-1.0)/A.nc would restrict the
maximum number of fill to the average number of nonzeros of A per column
(or per row) times the ELBOW. Note however that this parameter cuts off
the fill in S by brute force. It recommended NOT to use it.
|
| param.typetv |
Type of test vector.
for some PDE-based problems it might be sensible to ensure that the ILU
is exact when being applied to some given test vector. By default this
option is disabled ("none"). If you want to use this feature you can
either use "static" to pass a fixed test vector to the ILU. Or you can
use any other string. In this case, using reverse communication
principle, on every level you need to pass a test vector to the ILU. The
ILU passes to you the current coarse grid system and an initial guess for
the test vector. You have to return your own test vector. On entry to the
first level, this initial guess is simply the test vector you prescribed.
On any subsequent level, this will be your old test vector restricted to
the coarse grid.
|
| param.tv |
Test vector.
If you decide to pass a test vector, then pass the associated pointer.
ILUPACK will make its own copy inside AMGfactor, and you can release the
memory if you like. In PDE-based applications, a typical guess is the
vector with all ones.
|
| param.amg |
type of algebraic multilevel method
| "ilu"(default) | multilevel ILU
|
| "amli" | on each coarse grid, an inner iteration is used based on
flexible iterative solvers (e.g. fGMRES) to solve the inner coarse grid system,
preconditioned by the associated ILU. Note that this
requires to maintain all coarse grid systems and increases
the amount of memory. |
| "mg" | full multigrid with pre- and post smoothing, V-cycle,
W-cycle or flexible cycle is chosen. Essentially, the
multilevel ILU is used to define interpolation and
restriction operators as well as the coarse grid systems,
while the other components are set up as in the usual
multigrid framework. Not that the flexible cycle does not
pre-select the number of coarse grid solves a priori (e.g.
(1 for V-cycle, 2 for W-cycle), but on on each coarse grid,
an inner iteration is used based on flexible solvers to solve
the inner coarse grid system, preconditioned by the
associated full multigrid solver. Note that this type of
multigrid preconditioning requires to maintain all coarse
grid systems and increases the amount of memory.
|
|
| param.npresmoothing |
Number of pre-smoothing steps.
If classical multigrid is selected (param.amg="mg";), then here you can
set the number of pre-smoothing steps. default: 1
|
| param.npostsmoothing |
Number of post-smoothing steps.
If classical multigrid is selected (param.amg="mg";), then here you can
set the number of post-smoothing steps. default: 1
|
| param.ncoarse |
Number of coarse grid solves.
Except for multilevel ILU (i.e. param.amg="amli"; or param.amg="mg";),
here you define how often the coarse grid solve is performed. By default,
only one coarse grid solve is used (V-cycle). The choice param.ncoarse=2;
would correspond to a W-cycle. Note however, if a negative value is
passed, a flexible solver is invoked, i.e. the number of coarse grid
solves varies from one grid to another and from one step to the next one.
|
| param.presmoother |
Type of pre-smoother.
If full multigrid is used (param.amg="mg";), then here you can choose
between built-in smoothers or your own hand-made smoother.
| (a) |
"gsf"(default) |
Gauss-Seidel forward |
| (b) |
"gsb" |
Gauss-Seidel backward
|
| (c) |
"j" |
(damped) Jacobi |
| (d) |
"ilu" |
ILU on the fine grid system |
| (e) |
any other string that does not match (a)-(d) will cause AMGsolver
to use reverse communication principle in order to let you provide
your own smoother. In that case ILUPACK will give you the matrix,
the right hand side and an initial solution (typically 0). You have
to override the initial solution
|
|
| param.postsmoother |
Type of post-smoother.
If full multigrid is used (param.amg="mg";), then here you can choose
between built-in smoothers or your own hand-made smoother.
| (a) |
"gsf" |
Gauss-Seidel forward |
| (b) |
"gsb"(default) |
Gauss-Seidel backward
|
| (c) |
"j" |
(damped) Jacobi |
| (d) |
"ilu" |
ILU on the fine grid system |
| (e) |
any other string that does not match (a)-(d) will cause AMGsolver
to use reverse communication principle in order to let you provide
your own smoother. In that case ILUPACK will give you the matrix,
the right hand side and an initial solution (typically 0). You have
to override the initial solution
|
|
| param.FCpart |
Pre-selection of coarse grid nodes.
In some PDE-based applications it might be useful to select some coarse
grid nodes in advance. Essentially this strategy uses a Ruge-Stueben-like
heuristic strategy. If a test vector is available, the coarsening
strategy is applied to the matrix, which is diagonally scaled from the
right with the test vector.
| (a) |
"none"(default) |
leave the coarsening process to ILUPACK,
inverse-based strategy will construc a coarse grid on its
own. |
| (a) |
"yes" |
Some nodes are pre-selected as coarse grid nodes, ILUPACK
might add some further nodes. |
|
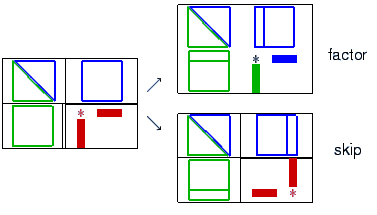
| param.typecoarse |
Type of coarse grid system.
By default the coarse grid system S is computed from A and the ILU in
|
typical ILU manner, i.e. if A
|
~
|
/ | L11 | 0 | \ | / | D11 | 0 | \ | / | U11 | U12 | \ |
then S |
| | | | | | | | | | | | | | | | | |, |
| \ | L21 | I | / | \ | 0 | S | / | \ | 0 | I | / |
is defined via S:= A22-L21*D11*U12.
Alternatively one could compute W21 ~ L21*L11^{-1}, Z12 ~ U11^{-1}*U12
|
and define S via S:= [-W21 I]*A*
|
/ | -Z12 | \ |
. This would refer to an AMG-like
|
| | | | | |
| \ | I | / |
strategy to compute a coarse grid system.
available are
| (a) |
"ilu"(default) |
ILU-type coarse grid system |
| (a) |
"amg" |
AMG-type coarse grid system |
|
| param.nrestart |
Number of steps before GMRES is restarted.
The iterative solver uses restarted GMRES (resp. fGMRES). By default, 30
steps are computed, before the method is restarted. Note that a smaller
number reduces the memory, while a larger number can improve the
convergence.
|
| param.mixedprecision |
require the computation of the preconditioner in
single precision
|
| param.contraction |
contraction factor < 1 of the residual for inner flexible solver when AMLI or
classical multigrid is used and options.ncoarse<0 (flexible coarse
grid solver)
|
| param.coarsereduce |
If different from zero, then the L21 and the U12 block
are discarded solving with L,U is done implicitly via L11,U11 and
A21 (resp. A12). If set to zero, then L21, U12 are kept
default: 1.
|
| param.decoupleconstraints |
This allows for saddle point type problems to explictly
decouple the connections between the constraint part and the
free part. Applied on every level, this allows for smaller coarse
grid matrices. If set to zero, then the additional decoupling is
not applied.
default: 1.
|
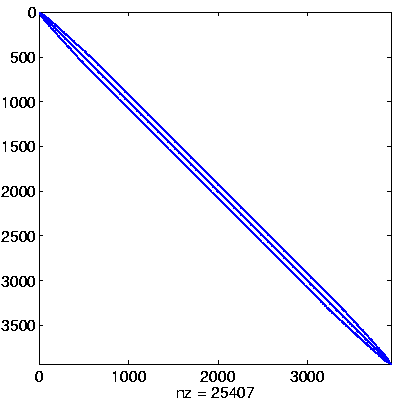
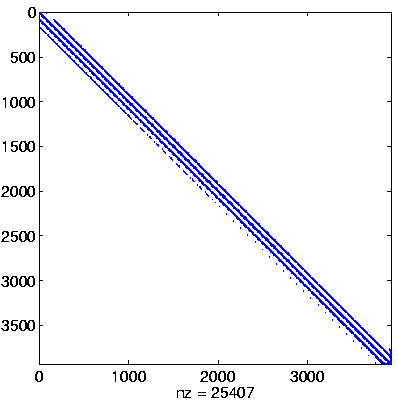
| Level 1 |
|
Initial system
|
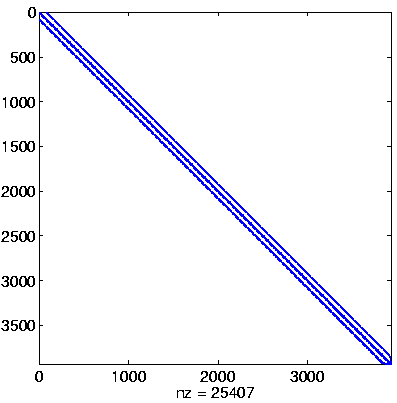
|
|
Initial system, reordered
here: no permutation
(no initial preprocessing)
|

|
|
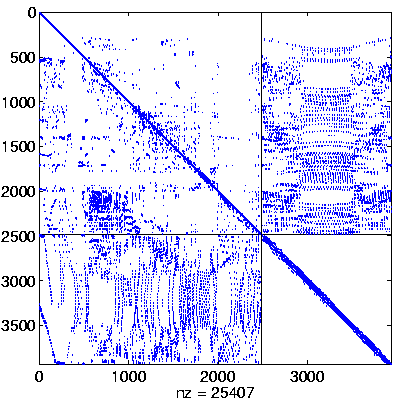
Initial Level, reordered after inverse-based ILU has been applied
|
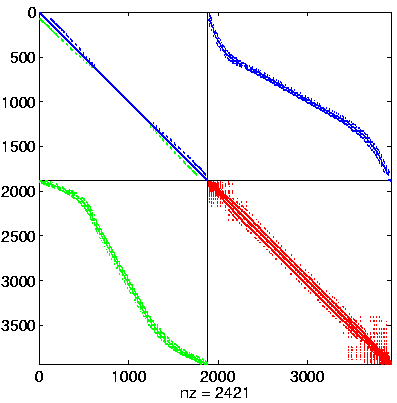
|
|
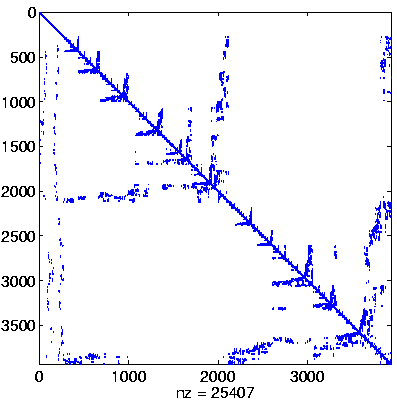
| Level 2 |
Level 2
Initial system |
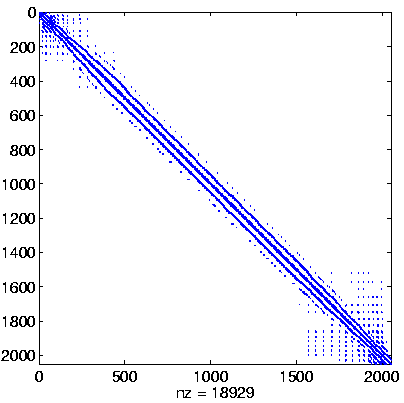
|
|
Level 2, reordered
(Reverse Cuthill-McKee,
regular reordering) |
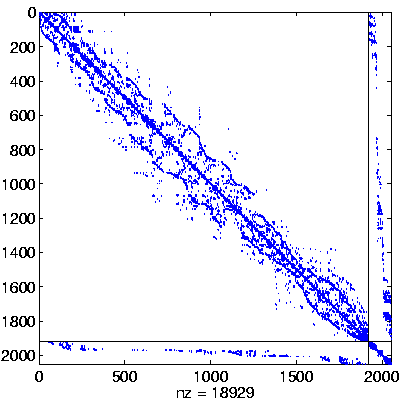
|
|
Level 2, reordered after inverse-based ILU has been applied |
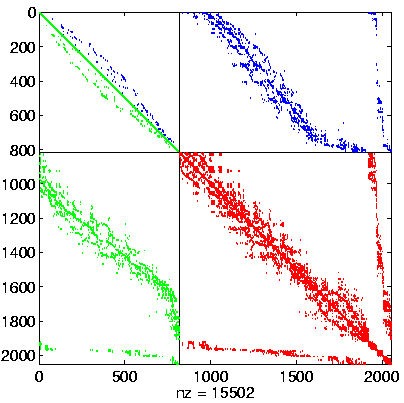
|
|
| Level 3 |
Level 3
Initial system |
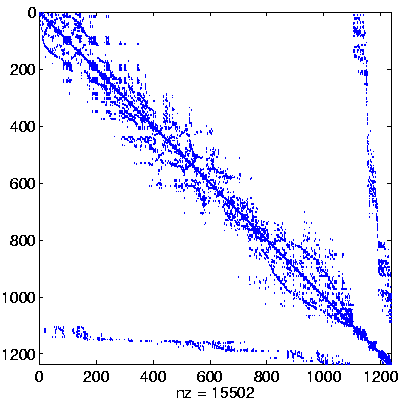
|
|
Level 3, reordered
(Reverse Cuthill-McKee,
regular reordering) |
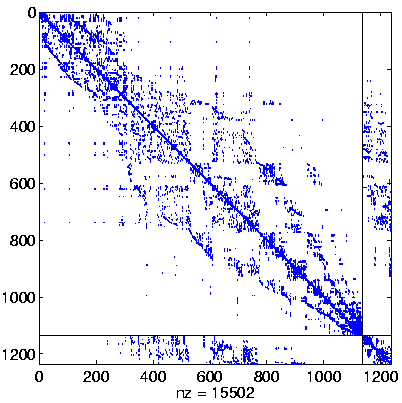
|
|
Level 3, reordered after inverse-based ILU has been applied |
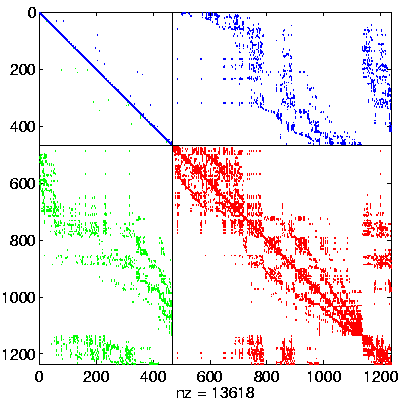
|
|
| Level 4 |
Level 4
Initial system |
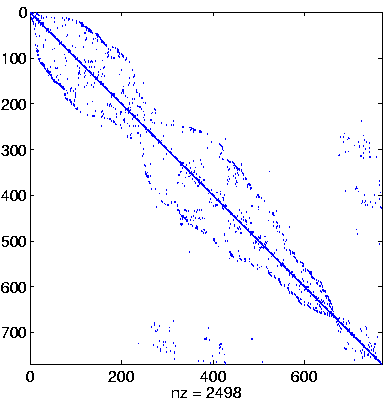
|
|
Level 4, reordered
(Reverse Cuthill-McKee,
regular reordering) |
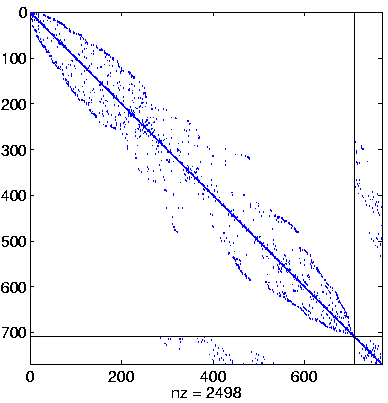
|
|
Level 4, reordered after inverse-based ILU has been applied |
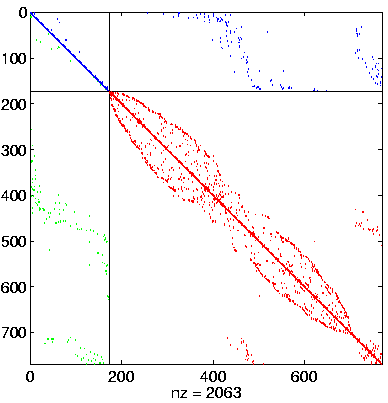
|
|
| Level 4 |
Level 4,
reordered again.
here ddPQ
(switched to final pivoting) |
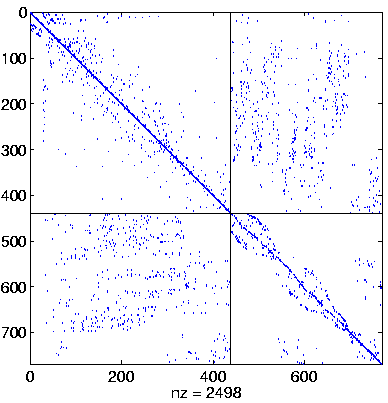
|
|
Level 4, reordered after inverse-based ILU has been applied |
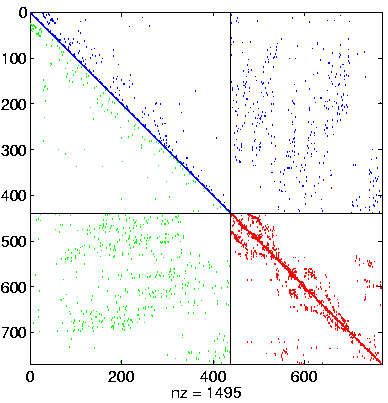
|