Theoretical Background

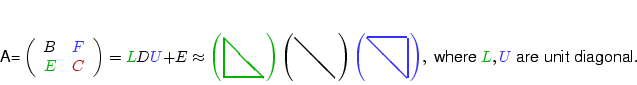
OBJECTIVE

Numerical solution of large sparse linear systems

Ax=b.

---

SOLUTION APPROACH

Preconditioned iterative solver (Krylov subspace method, e.g. GMRES)

---

PRECONDITIONER

Incomplete LU decomposition methods

---

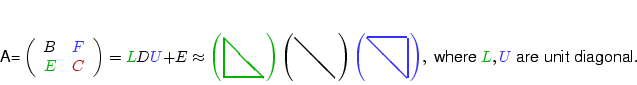
RULE OF THUMB

Iterative solvers perform quite well if , where (strict for certain iterative solvers like GMRES)

---

PARTIAL INCOMPLETE LU DECOMPOSITION

k steps of an incomplete LU decomposition

where , are unit diagonal, reduced matrix (``approximate Schur complement''). The leading part of is diagonal.

---

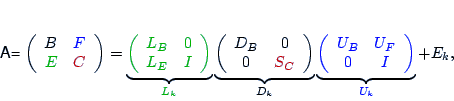
LEVEL-BASED ILUS

has a specific nonzero pattern.

---

THRESHOLD-ORIENTED ILUS

, drop tolerance.

---

GROWTH OF THE INVERSE TRIANGULAR FACTORS

and may become very large pivoting recommended.

What kind of pivoting is appropriate?

---

INVERSE ERROR

For preconditioning we have to apply

-->

Denote by

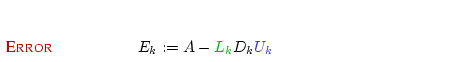
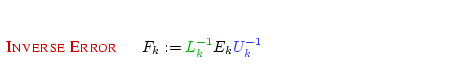
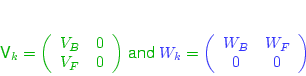
the entries being dropped from and .

Lemma[B.,Saad '04]. Error bounds for the inverse error .

1. Standard case, e.g. [Meijerink & Van der Vorst '77, Munksgaard '80, Saad '94]
   
   
2. There exists an ILU (``Tismenetsky approach'') such that
   

1. Standard case
   
2. Tismenetsky case
   
   

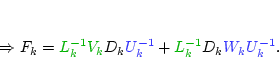
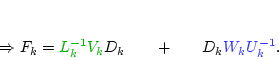
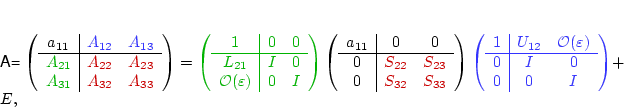
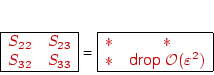
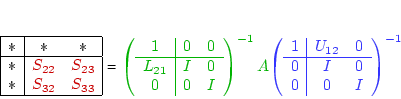
CONSEQUENCES

• and contribute to the inverse error
• For the standard case even their PRODUCT !

PRECONDITIONED ITERATIVE SOLVERS

Solve instead of , where

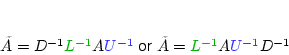
DRAWBACK

Preconditioned system requires or to be small.

THRESHOLD-ORIENTED ILUS

, drop tolerance

INVERSE-BASED APPROACH

Prescribe a bound and apply diagonal pivoting such that and .

FACTOR OR SKIP STRATEGY

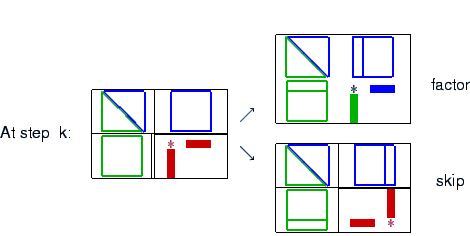
Rows/columns that exceed the prescribed bound are pushed to the end